Chernik Referencias Menú de navegación43°48′29″N 27°07′00″E / 43.808055555556, 27.11666666666743°48′29″N 27°07′00″E / 43.808055555556, 27.116666666667Преброяване на населението, 01.02.2011, НСИMapa de Chernik

Localidades de la provincia de SilistraMunicipio de Dulovo


búlgaropuebloBulgariamunicipio de Dulovoprovincia de SilistraDulovoturcosDulovoRuse


























Chernik
Черник

Pueblo



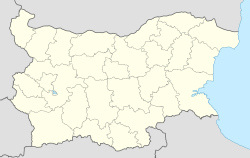Chernik ubicada en Bulgaria

Chernik

Chernik





Localización de Chernik en Bulgaria

Coordenadas
43°48′29″N 27°07′00″E / 43.808055555556, 27.116666666667Coordenadas: 43°48′29″N 27°07′00″E / 43.808055555556, 27.116666666667
Entidad
Pueblo
 • País

Bandera de Bulgaria Bulgaria
 • Provincia

Silistra
 • Municipio

Dulovo
Altitud
 
 • Media
232 m s. n. m.

Población (15 de marzo de 2015)
 
 • Total
2520 hab.
Huso horario
UTC+02:00 y UTC+03:00
Código postal
7651
[editar datos en Wikidata]

Chernik (búlgaro: Черник) es un pueblo de Bulgaria perteneciente al municipio de Dulovo de la provincia de Silistra.


Con 2343 habitantes en 2011, es la segunda localidad más importante del municipio tras la capital municipal Dulovo.[1]​


La localidad está habitada principalmente por turcos de origen qizilbash. El principal monumento de la localidad es una türbe construida en 1994.[2]​ La fiesta local del pueblo es el 6 de mayo.


Se ubica en la periferia occidental de la capital municipal Dulovo, en la salida de dicha ciudad por la carretera 23 que lleva a Ruse.[3]​



Referencias



  1. ↑ Преброяване на населението, 01.02.2011, НСИ


  2. ↑ Миков, Любомир (2007). Култова архитектура и изкуство на хетеродоксните мюсюлмани в България (XVI-XX век). София: Академично издателство „Проф. Марин Дринов“. pp. 118-120. ISBN 978-954-322-197-4. 


  3. ↑ Mapa de Chernik







-

Popular posts from this blog

Virtualbox - Configuration error: Querying “UUID” failed (VERR_CFGM_VALUE_NOT_FOUND)“VERR_SUPLIB_WORLD_WRITABLE” error when trying to installing OS in virtualboxVirtual Box Kernel errorFailed to open a seesion for the virtual machineFailed to open a session for the virtual machineUbuntu 14.04 LTS Virtualbox errorcan't use VM VirtualBoxusing virtualboxI can't run Linux-64 Bit on VirtualBoxUnable to insert the virtual optical disk (VBoxguestaddition) in virtual machine for ubuntu server in win 10VirtuaBox in Ubuntu 18.04 Issues with Win10.ISO Installation

Image
Fear of getting stuck on one programming language / technology that is not used in my country Do the primes contain an infinite almost arithmetic progression? Biological Blimps: Propulsion Are Captain Marvel's powers affected by Thanos' actions in Infinity War Why does AES have exactly 10 rounds for a 128-bit key, 12 for 192 bits and 14 for a 256-bit key size? Can a College of Swords bard use a Blade Flourish option on an opportunity attack provoked by their own Dissonant Whispers spell? Can disgust be a key component of horror? Can I say "fingers" when referring to toes? What is Cash Advance APR? Why Shazam when there is already Superman? What does "Scientists rise up against statistical significance" mean? (Comment in Nature) What does chmod -u do? What should you do when eye contact makes your subordinate uncomfortable? Issue while creating Apex class using API How much character growth crosses the line into breaking the charac...
Read more

How to disable autoformat in LibreOffice 6 Calc?Updating LibreOffice Calc 3.3.4How to run Libreoffice calcLibreOffice Calc - Disable roundingLibreoffice calc date format problemSimple query in LibreOffice Calclibreoffice calc -copy paste not workingExpand LibreOffice calc filter boxLibreOffice Calc Macro doesn't insert new sheetLibreoffice Calc Today Function Date Format?LibreOffice Calc - Delete empty rows

Image
What if you are holding an Iron Flask with a demon inside and walk into Antimagic Field? What are the balance implications behind making invisible things auto-hide? Calculating total slots What exact color does ozone gas have? Multiplicative persistence Does the UK parliament need to pass secondary legislation to accept the Article 50 extension How to hide some fields of struct in C? How do I delete all blank lines in a buffer? How can mimic phobia be cured? Mimic lecturing on blackboard, facing audience Terse Method to Swap Lowest for Highest? Why does the Sun have different day lengths, but not the gas giants? Strong empirical falsification of quantum mechanics based on vacuum energy density Why is the "ls" command showing permissions of files in a FAT32 partition? Quoting Keynes in a lecture How do apertures which seem too large to physically fit work? What is Cash Advance APR? Fear of getting stuck on one programming language / technology...
Read more

When should I use the pronoun “ri”?What is the meaning of “korekta” and when to use it?How do I know when to use the preposition “je”?When to use “olda” instead of “maljuna”?When should I use “tio” and “tiu”?When should I use “tiam, kiam” instead of just “kiam”?Should I ever use the pronoun “ci”?What words for different levels of education should I use?When to use “ĝin” and “tion”When should I use “tion, kion” or just “kion”?Why is there no plural “kio,” like “kioj?”

Image
If I can solve Sudoku, can I solve the Travelling Salesman Problem (TSP)? If so, how? Welcoming 2019 Pi day: How to draw the letter π? What is "focus distance lower/upper" and how is it different from depth of field? A diagram about partial derivatives of f(x,y) Examples of transfinite towers Why does overlay work only on the first tcolorbox? As a new Ubuntu desktop 18.04 LTS user, do I need to use ufw for a firewall or is iptables sufficient? Adventure Game (text based) in C++ Can I use USB data pins as power source Instead of a Universal Basic Income program, why not implement a "Universal Basic Needs" program? Is there a place to find the pricing for things not mentioned in the PHB? (non-magical) Fastest way to pop N items from a large dict combinatorics floor summation What is the Japanese sound word for the clinking of money? Why did it take so long to abandon sail after steamships were demonstrated? Python if-else code style for r...
Read more