Neubeuern
Referencias
Enlaces externos
Menú de navegación47°46′00″N 12°09′00″E / 47.766666666667, 12.1547°46′00″N 12°09′00″E / 47.766666666667, 12.15Sitio web oficial Citypopulation.de
Multi tool useLocalidades del distrito de Rosenheim
distritoRosenheimestado federadoBavieraregiónAlta BavieraAlpesAustriarío EnoDanubio
| Neubeuern |
|---|
Municipio |
|
Escudo
|
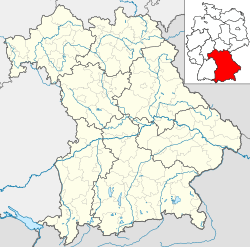Ubicación en el estado de Baviera
|
Ubicación en el distrito
|
| Coordenadas |
47°46′00″N 12°09′00″E / 47.766666666667, 12.15Coordenadas: 47°46′00″N 12°09′00″E / 47.766666666667, 12.15
|
|---|
| Entidad |
Municipio |
|---|
• País
|
 Alemania
|
|---|
• Estado
|
Baviera
|
|---|
• Región
|
Alta Baviera
|
|---|
• Distrito
|
Rosenheim
|
|---|
| Superficie |
|
|---|
| • Total |
15,32 km² 
|
|---|
| Altitud |
|
|---|
| • Media |
478 m s. n. m.
|
|---|
Población (25 de mayo de 1987) |
|
|---|
| • Total |
3358 hab. |
|---|
• Densidad
|
219,19 hab/km² |
|---|
| Huso horario |
UTC+01:00 y UTC+02:00 |
|---|
| Código postal |
83115
|
|---|
| Prefijo telefónico |
08035 |
|---|
| Matrícula |
RO |
|---|
| Número oficial de comunidad |
09187154 |
|---|
Sitio web oficial
|
[editar datos en Wikidata] |
Neubeuern es un municipio situado en el distrito de Rosenheim, en el estado federado de Baviera (Alemania), con una población a finales de 2016 de unos 4387 habitantes.[1]
Se encuentra ubicado al sur del estado, en la región de Alta Baviera, en la ladera de los Alpes, cerca de la frontera con Austria y de la orilla del río Eno —un afluente derecho del Danubio—.
Referencias
↑ Citypopulation.de Estadísticas del distrito de Rosenheim. Consultado el 28 de junio de 2018
Enlaces externos
Wikimedia Commons alberga una categoría multimedia sobre Neubeuern.
KD4Jfz38Cx52FF29hETu4GfAfIO8q97DNmoYFCsVNAXUxgR3qSe3cKts6ITHV2bc7Fdv3966Q,vNTMx1SJGt,y jyl9de,zlfz
Popular posts from this blog
Fear of getting stuck on one programming language / technology that is not used in my country Do the primes contain an infinite almost arithmetic progression? Biological Blimps: Propulsion Are Captain Marvel's powers affected by Thanos' actions in Infinity War Why does AES have exactly 10 rounds for a 128-bit key, 12 for 192 bits and 14 for a 256-bit key size? Can a College of Swords bard use a Blade Flourish option on an opportunity attack provoked by their own Dissonant Whispers spell? Can disgust be a key component of horror? Can I say "fingers" when referring to toes? What is Cash Advance APR? Why Shazam when there is already Superman? What does "Scientists rise up against statistical significance" mean? (Comment in Nature) What does chmod -u do? What should you do when eye contact makes your subordinate uncomfortable? Issue while creating Apex class using API How much character growth crosses the line into breaking the charac...
Localidades de Baden-Wurtemberg municipioalemándistrito de LuisburgoBaden-WurtembergLuisburgoCasa de WurtembergGuerra de los Treinta AñosGuerra de los Nueve Años Möglingen Municipio Iglesia gótica de San Pancracio. Escudo Möglingen Localización de Möglingen en Alemania Ubicación de Möglingen Coordenadas 48°53′18″N 9°07′45″E / 48.888333333333, 9.1291666666667 Coordenadas: 48°53′18″N 9°07′45″E / 48.888333333333, 9.1291666666667 Entidad Municipio • País Alemania • Estado Baden-Wurtemberg • Distrito Luisburgo Superficie • Total 9,93 km², 9,95 km² y 9,93 km² Altitud • Media 297 m s. n. m. Población (2014) • Total 10 983 hab. • Densidad Expresión errónea: car...
Nacidos en 1590Fallecidos en 1665HombresArzobispos Primados de MéxicoCapitalinos (México)Obispos de México del siglo XVIIObispos nombrados por Alejandro VII Ciudad de México25 de noviembre1590ibídem2 de septiembre1665mexicanocriollocátedraTeologíacapellánCarmelitas descalzasCiudad de México1635Puebla de los ÁngelesOaxacaCuevascatedralesPueblaArzobispoArzobispo de MéxiconoblesclérigosCorona Alfonso de Cuevas Dávalos, grabado calcográfico de Antonio Onofre Moreno. Biblioteca Nacional de España. Juan Alonso de Cuevas Dávalos , (Ciudad de México, 25 de noviembre de 1590 - ibídem, 2 de septiembre de 1665) fue un arzobispo mexicano. Índice 1 Biografía 2 Grados y cargos 3 Referencias 4 Bibliografía Biografía De padres ligados a los círculos nobiliarios del virreinato, Alonso de Cuevas nació en Ciudad de México [ 1 ] (y por ende criollo). Comenzó sus es...
Alemania
Wikimedia Commons alberga una categoría multimedia sobre Neubeuern.
