Vonges Demografía Enlaces externos Menú de navegación47°17′32″N 5°23′58″E / 47.292222222222, 5.399444444444447°17′32″N 5°23′58″E / 47.292222222222, 5.3994444444444[Consultar]Institut géographique nationalINSEECódigo postal n.º 21270Datos de población para el año 2012
Localidades de Côte-d'Or
comuna francesaBorgoñadepartamentoCôte-d'Ordistrito de Dijoncantón de Pontailler-sur-Saône
| Vonges | ||
|---|---|---|
Entidad subnacional | ||
 | ||
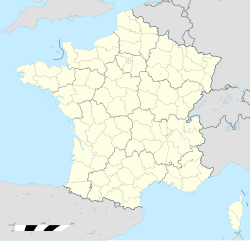 Vonges Localización de Vonges en Francia | ||
 Ubicación de Vonges | ||
| Coordenadas | 47°17′32″N 5°23′58″E / 47.292222222222, 5.3994444444444Coordenadas: 47°17′32″N 5°23′58″E / 47.292222222222, 5.3994444444444 | |
| Entidad | Comuna de Francia | |
| • País | ||
| • Región | Borgoña | |
| • Departamento | Côte-d'Or | |
| • Distrito | distrito de Dijon | |
| • Cantón | cantón de Pontailler-sur-Saône | |
| • Mancomunidad | Communauté de communes du Canton de Pontailler | |
| Alcalde | Gérard Pilard (2001-2008) | |
| Superficie | ||
| • Total | 4,56 km² | |
| Altitud | ||
| • Media | 214 m s. n. m. | |
| • Máxima | 207 m s. n. m. | |
| • Mínima | 182 m s. n. m. | |
Población (2015) | ||
| • Total | 353 hab. | |
| • Densidad | 77,41 hab/km² | |
| Huso horario | CET (UTC +1) | |
| • en verano | CEST (UTC +2) | |
| Código postal | 21270[1] | |
| Código INSEE | 21713[2] | |
Vonges es una población y comuna francesa, en la región de Borgoña, departamento de Côte-d'Or, en el distrito de Dijon y cantón de Pontailler-sur-Saône.
Demografía
| 1962 | 1968 | 1975 | 1982 | 1990 | 1999 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 712 | 612 | 504 | 325 | 283 | 313 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Para los censos de 1962 a 1999 la población legal corresponde a la población sin duplicidades (Fuente: INSEE [Consultar]) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Enlaces externos
- Institut géographique national
INSEE
↑ worldpostalcodes.org,
Código postal n.º 21270 (en francés)
↑ INSEE, Datos de población para el año 2012 de Vonges (en francés)