Oak Glen (California)
Geografía
Referencias
Enlaces externos
Menú de navegación34°02′44″N 116°56′59″O / 34.045555555556, -116.9497222222234°02′44″N 116°56′59″O / 34.045555555556, -116.9497222222234°2′44.14″N 116°56′58.62″O / 34.0455944, -116.9496167«Encuentra un condado»«American FactFinder»
Multi tool useLocalidades del condado de San BernardinoLugares designados por el censo en California
lugar designado por el censocondado de San Bernardinoestado estadounidenseCalifornia2010
| Oak Glen |
|---|
Lugar designado por el censo
|
|
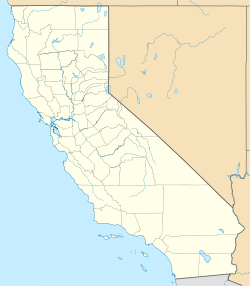Ubicación en el condado de San Bernardino en California
|
Ubicación de California en EE. UU.
|
| Coordenadas |
34°02′44″N 116°56′59″O / 34.045555555556, -116.94972222222Coordenadas: 34°02′44″N 116°56′59″O / 34.045555555556, -116.94972222222
|
|---|
| Entidad |
Lugar designado por el censo
|
|---|
• País
|
 Estados Unidos
|
|---|
• Estado
|
 California
|
|---|
• Condado
|
San Bernardino
|
|---|
| Fundación |
31 de marzo de 2010
|
|---|
| Superficie |
|
|---|
| • Total |
38,51 km² 
|
|---|
| Altitud |
|
|---|
| • Media |
1443 m s. n. m.
|
|---|
Población (2010) |
|
|---|
| • Total |
638 hab. |
|---|
• Densidad
|
16,57 hab/km² |
|---|
| Huso horario |
Pacífico: UTC-8
|
|---|
• en verano
|
UTC-7
|
|---|
| Código ZIP |
92399
|
|---|
| Código de área |
909 |
|---|
[editar datos en Wikidata] |
Oak Glen es un lugar designado por el censo ubicado en el condado de San Bernardino en el estado estadounidense de California. En el año 2010 tenía una población de 638 habitantes.[1]
Geografía
Oak Glen se encuentra ubicado en las coordenadas 34°2′44.14″N 116°56′58.62″O / 34.0455944, -116.9496167.[2]
Referencias
↑ «Encuentra un condado» (en inglés). Asociación Nacional de Condados. 2 de mayo de 2013. Consultado el 2 de mayo de 2013.
↑ «American FactFinder» (en inglés). Oficina del Censo de los Estados Unidos. Consultado el 2 de mayo de 2013.
Enlaces externos
Portal:California. Contenido relacionado con California.
Wikimedia Commons alberga una categoría multimedia sobre Oak Glen.
tE,ZOGS
Popular posts from this blog
Fear of getting stuck on one programming language / technology that is not used in my country Do the primes contain an infinite almost arithmetic progression? Biological Blimps: Propulsion Are Captain Marvel's powers affected by Thanos' actions in Infinity War Why does AES have exactly 10 rounds for a 128-bit key, 12 for 192 bits and 14 for a 256-bit key size? Can a College of Swords bard use a Blade Flourish option on an opportunity attack provoked by their own Dissonant Whispers spell? Can disgust be a key component of horror? Can I say "fingers" when referring to toes? What is Cash Advance APR? Why Shazam when there is already Superman? What does "Scientists rise up against statistical significance" mean? (Comment in Nature) What does chmod -u do? What should you do when eye contact makes your subordinate uncomfortable? Issue while creating Apex class using API How much character growth crosses the line into breaking the charac...
Localidades de Baden-Wurtemberg municipioalemándistrito de LuisburgoBaden-WurtembergLuisburgoCasa de WurtembergGuerra de los Treinta AñosGuerra de los Nueve Años Möglingen Municipio Iglesia gótica de San Pancracio. Escudo Möglingen Localización de Möglingen en Alemania Ubicación de Möglingen Coordenadas 48°53′18″N 9°07′45″E / 48.888333333333, 9.1291666666667 Coordenadas: 48°53′18″N 9°07′45″E / 48.888333333333, 9.1291666666667 Entidad Municipio • País Alemania • Estado Baden-Wurtemberg • Distrito Luisburgo Superficie • Total 9,93 km², 9,95 km² y 9,93 km² Altitud • Media 297 m s. n. m. Población (2014) • Total 10 983 hab. • Densidad Expresión errónea: car...
Nacidos en 1590Fallecidos en 1665HombresArzobispos Primados de MéxicoCapitalinos (México)Obispos de México del siglo XVIIObispos nombrados por Alejandro VII Ciudad de México25 de noviembre1590ibídem2 de septiembre1665mexicanocriollocátedraTeologíacapellánCarmelitas descalzasCiudad de México1635Puebla de los ÁngelesOaxacaCuevascatedralesPueblaArzobispoArzobispo de MéxiconoblesclérigosCorona Alfonso de Cuevas Dávalos, grabado calcográfico de Antonio Onofre Moreno. Biblioteca Nacional de España. Juan Alonso de Cuevas Dávalos , (Ciudad de México, 25 de noviembre de 1590 - ibídem, 2 de septiembre de 1665) fue un arzobispo mexicano. Índice 1 Biografía 2 Grados y cargos 3 Referencias 4 Bibliografía Biografía De padres ligados a los círculos nobiliarios del virreinato, Alonso de Cuevas nació en Ciudad de México [ 1 ] (y por ende criollo). Comenzó sus es...
Estados Unidos
California
Portal:California. Contenido relacionado con California.
Wikimedia Commons alberga una categoría multimedia sobre Oak Glen.
