Roggenburg Referencias Enlaces externos Menú de navegación47°26′00″N 7°20′00″E / 47.433333333333, 7.333333333333347°26′00″N 7°20′00″E / 47.433333333333, 7.3333333333333Sitio web oficial«Bilanz der ständigen Wohnbevölkerung nach Bezirken und Gemeinden»Sitio oficial de la comuna de Roggenburgalemánfrancésitaliano

Comunas de Basilea-Campiña


francéscomunasuizacantón de Basilea-Campiñadistrito de LaufenKiffisFRA68KleinlützelSOLiesbergSoyhièresJUMovelierJUEderswilerJUPleigneJU


























Roggenburg

comuna de Suiza

Wappen Roggenburg BL.png
Escudo





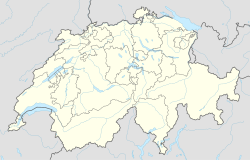Roggenburg ubicada en Suiza

Roggenburg

Roggenburg





Localización de Roggenburg en Suiza
País
Bandera de Suiza Suiza
• Cantón

Bandera de Cantón de Basilea-Campiña Basilea-Campiña
• Distrito

Laufen
Ubicación
47°26′00″N 7°20′00″E / 47.433333333333, 7.3333333333333Coordenadas: 47°26′00″N 7°20′00″E / 47.433333333333, 7.3333333333333
• Altitud

438 msnm
Superficie
6,65 km²

Población[1]​
291 hab. (2014)
• Densidad

44 hab./km²
Lengua
Alemán
Código postal
2814
Sitio web
Sitio web oficial
[editar datos en Wikidata]


Roggenburg (en francés Roggenbourg, hispanizado Roggemburgo) es una comuna suiza del cantón de Basilea-Campiña, situada en el distrito de Laufen. Limita al norte con la comuna de Kiffis (FRA-68), al este con Kleinlützel (SO), al sureste con Liesberg, al sur con Soyhières (JU) y Movelier (JU), al suroeste con Ederswiler (JU), y al noroeste con Pleigne (JU).



Referencias



  1. ↑ Oficina federal de estadística (31 de diciembre de 2014). «Bilanz der ständigen Wohnbevölkerung nach Bezirken und Gemeinden» (en alemán). Consultado el 19 de noviembre de 2015. 



Enlaces externos



  • Wikimedia Commons alberga una categoría multimedia sobre Roggenburg.

  • Sitio oficial de la comuna de Roggenburg


  • Roggenburg en alemán, francés o italiano en el Diccionario histórico de Suiza.


-

Popular posts from this blog

Möglingen Índice Localización Historia Demografía Referencias Enlaces externos Menú de navegación48°53′18″N 9°07′45″E / 48.888333333333, 9.129166666666748°53′18″N 9°07′45″E / 48.888333333333, 9.1291666666667Sitio web oficial Mapa de Möglingen«Gemeinden in Deutschland nach Fläche, Bevölkerung und Postleitzahl am 30.09.2016»Möglingen

Image
Localidades de Baden-Wurtemberg municipioalemándistrito de LuisburgoBaden-WurtembergLuisburgoCasa de WurtembergGuerra de los Treinta AñosGuerra de los Nueve Años Möglingen Municipio Iglesia gótica de San Pancracio. Escudo Möglingen Localización de Möglingen en Alemania Ubicación de Möglingen Coordenadas 48°53′18″N 9°07′45″E  /  48.888333333333, 9.1291666666667 Coordenadas: 48°53′18″N 9°07′45″E  /  48.888333333333, 9.1291666666667 Entidad Municipio  • País   Alemania  • Estado Baden-Wurtemberg  • Distrito Luisburgo Superficie    • Total 9,93 km², 9,95 km² y 9,93 km² Altitud    • Media 297 m s. n. m. Población (2014)    • Total 10 983 hab.  • Densidad Expresión errónea: car...
Read more

Virtualbox - Configuration error: Querying “UUID” failed (VERR_CFGM_VALUE_NOT_FOUND)“VERR_SUPLIB_WORLD_WRITABLE” error when trying to installing OS in virtualboxVirtual Box Kernel errorFailed to open a seesion for the virtual machineFailed to open a session for the virtual machineUbuntu 14.04 LTS Virtualbox errorcan't use VM VirtualBoxusing virtualboxI can't run Linux-64 Bit on VirtualBoxUnable to insert the virtual optical disk (VBoxguestaddition) in virtual machine for ubuntu server in win 10VirtuaBox in Ubuntu 18.04 Issues with Win10.ISO Installation

Image
Fear of getting stuck on one programming language / technology that is not used in my country Do the primes contain an infinite almost arithmetic progression? Biological Blimps: Propulsion Are Captain Marvel's powers affected by Thanos' actions in Infinity War Why does AES have exactly 10 rounds for a 128-bit key, 12 for 192 bits and 14 for a 256-bit key size? Can a College of Swords bard use a Blade Flourish option on an opportunity attack provoked by their own Dissonant Whispers spell? Can disgust be a key component of horror? Can I say "fingers" when referring to toes? What is Cash Advance APR? Why Shazam when there is already Superman? What does "Scientists rise up against statistical significance" mean? (Comment in Nature) What does chmod -u do? What should you do when eye contact makes your subordinate uncomfortable? Issue while creating Apex class using API How much character growth crosses the line into breaking the charac...
Read more

Torre de la Isleta Índice Véase también Referencias Bibliografía Enlaces externos Menú de navegación38°25′58″N 0°23′02″O / 38.43277778, -0.3838888938°25′58″N 0°23′02″O / 38.43277778, -0.38388889Torre de la Illeta de l’Horta o Torre Saleta. Base de datos de bienes inmuebles. Patrimonio Cultural. Secretaría de Estado de CulturaFicha BIC Torre de la Illeta de l’Horta. Dirección General de Patrimonio Cultural. Generalitat ValencianaLugares de interés. Ayuntamiento del CampelloTorre de la Isleta en CastillosNet.org

Image
Bienes de interés cultural de la provincia de AlicanteTorres defensivas de la provincia de AlicanteCampo de AlicanteTorres defensivas de la Comunidad Valenciana en el siglo XVICampello siglo XVICampelloprovincia de AlicanteEspañayacimiento arqueológico de La IsletabóvedamamposteríasillarejosilleríaménsulasVirrey de ValenciaBernardino de Cárdenas y Pachecoduque de Maquedapiratas berberiscosCastillo de Santa BárbaraAlicanteTorre de AguasCampelloBien de Interés Cultural Torre de la Isleta Torre de la Illeta Bien de Interés Cultural Patrimonio histórico de España Vista de la Torre Declaración 12 de febrero de 1996 Figura de protección Monumento Código RI-51 - 0009165 - 00000 [ 1 ] ​ Coordenadas 38°25′58″N 0°23′02″O  /  38.43277778, -0.38388889 Coordenadas: 38°25′58″N 0°23′02″O  /  38.43277778, -0.38388889 ...
Read more