Radimovice u Tábora Referencias Enlaces externos Menú de navegación49°27′27″N 14°38′21″E / 49.457386474039, 14.63905607821249°27′27″N 14°38′21″E / 49.457386474039, 14.639056078212Sitio web oficial Citypopulation.de

Localidades de la región de Bohemia Meridional


distrito de TáborregiónBohemia MeridionalRepública ChecaPragarío LužniceMoldavaElbaVysočinaBohemia Central
































Radimovice u Tábora

Localidad

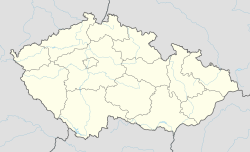Radimovice u Tábora (08).jpg




Radimovice u Tábora ubicada en República Checa

Radimovice u Tábora

Radimovice u Tábora





Localización de Radimovice u Tábora en República Checa

Coordenadas
49°27′27″N 14°38′21″E / 49.457386474039, 14.639056078212Coordenadas: 49°27′27″N 14°38′21″E / 49.457386474039, 14.639056078212
Entidad
Localidad
 • País

Bandera de República Checa República Checa
 • Región

Bohemia Meridional
 • Distrito
Tábor
Superficie
 
 • Total
2,67 km² Ver y modificar los datos en Wikidata
Altitud
 
 • Media
487 m s. n. m.

Población (1 de enero de 2018)
 
 • Total
63 hab.
 • Densidad

23,63 hab/km²
Código postal
391 31
Matrícula
TA

Sitio web oficial
[editar datos en Wikidata]

Radimovice u Tábora es una localidad del distrito de Tábor en la región de Bohemia Meridional, República Checa, con una población estimada a principio del año 2018 de 63 habitantes.


Se encuentra ubicada al noreste de la región, a poca distancia al sur de Praga, y cerca de la orilla del río Lužnice —un afluente del Moldava que, a su vez, es afluente del Elba— y de la frontera con las regiones de Vysočina y Bohemia Central.[1]​



Referencias



  1. ↑ Citypopulation.de Estadísticas del distrito de Tábor. Consultado el 29 de julio de 2018.



Enlaces externos



  • Wikimedia Commons alberga una categoría multimedia sobre Radimovice u Tábora.

-

Popular posts from this blog

Virtualbox - Configuration error: Querying “UUID” failed (VERR_CFGM_VALUE_NOT_FOUND)“VERR_SUPLIB_WORLD_WRITABLE” error when trying to installing OS in virtualboxVirtual Box Kernel errorFailed to open a seesion for the virtual machineFailed to open a session for the virtual machineUbuntu 14.04 LTS Virtualbox errorcan't use VM VirtualBoxusing virtualboxI can't run Linux-64 Bit on VirtualBoxUnable to insert the virtual optical disk (VBoxguestaddition) in virtual machine for ubuntu server in win 10VirtuaBox in Ubuntu 18.04 Issues with Win10.ISO Installation

Image
Fear of getting stuck on one programming language / technology that is not used in my country Do the primes contain an infinite almost arithmetic progression? Biological Blimps: Propulsion Are Captain Marvel's powers affected by Thanos' actions in Infinity War Why does AES have exactly 10 rounds for a 128-bit key, 12 for 192 bits and 14 for a 256-bit key size? Can a College of Swords bard use a Blade Flourish option on an opportunity attack provoked by their own Dissonant Whispers spell? Can disgust be a key component of horror? Can I say "fingers" when referring to toes? What is Cash Advance APR? Why Shazam when there is already Superman? What does "Scientists rise up against statistical significance" mean? (Comment in Nature) What does chmod -u do? What should you do when eye contact makes your subordinate uncomfortable? Issue while creating Apex class using API How much character growth crosses the line into breaking the charac...
Read more

Eliminatorias de Conmebol para la Copa Mundial de Fútbol de 2006 Índice Tabla de posiciones final Partidos Goleadores Repesca Intercontinental Clasificados Véase también Referencias Enlaces externos Menú de navegación2:0 (1:0)2:2 (2:0)4:1 (2:1)5:0 (2:0)1:2 (1:1)0:3 (0:3)2:1 (1:0)4:0 (2:0)4:1 (1:1)1:0 (1:0)2:1 (1:1)0:1 (0:1)2:1 (1:0)3:0 (0:0)1:1 (0:1)2:1 (0:0)0:1 (0:1)0:01:1 (0:1)3:3 (2:0)0:2 (0:1)1:0 (0:0)0:3 (0:1)0:00:2 (0:2)2:1 (1:1)0:1 (0:0)1:3 (0:2)2:1 (1:0)3:1 (1:0)3:2 (3:0)0:00:05:0 (3:0)1:1 (0:1)1:3 (0:1)1:0 (0:0)3:1 (3:0)1:0 (0:0)0:04:2 (3:0)1:0 (0:0)1:1 (1:0)2:5 (0:2)2:0 (0:0)0:01:1 (1:0)0:00:03:1 (1:1)3:2 (2:1)1:0 (1:0)2:1 (0:0)1:0 (0:0)1:0 (0:0)0:01:1 (0:1)1:2 (0:0)5:2 (2:2)1:0 (0:0)3:1 (2:0)2:1 (1:0)1:0 (0:0)2:2 (1:2)1:1 (0:0)3:1 (2:0)2:0 (0:0)1:1 (0:1)5:0 (1:0)4:1 (2:0)0:03:0 (2:0)2:1 (1:0)3:1 (3:0)4:1 (2:1)1:0 (1:0)4:1 (1:0)1:2 (1:1)5:0 (4:0)3:2 (1:0)0:00:1 (0:0)1:1 (1:0)1:1 (0:1)2:0 (0:0)1:0 (0:0)0:1 (0:1)0:03:0 (1:0)4:1 (3:0)ReporteReporteGoleadores de las Eliminatorias Sudamericanas 2006.Eliminatorias Sudamericanas 2006 - FIFAEliminatorias Sudamericanas 2006 - RSSSF

Image
Copa Mundial de Fútbol de 2006Fútbol en 2003Fútbol en 2004Fútbol en 2005Clasificación de Conmebol para la Copa Mundial de Fútbol de 2006 ConmebolOFCtodos contra todosArgentinaBrasilEcuadorParaguayUruguayAustraliaMontevideoSídneytripletasKewell Neill Vidmar Viduka Aloisi Rodríguez Varela Estoyanoff Zalayeta III Eliminatorias de Conmebol para la Copa Mundial de Fútbol 2003-2005       países clasificados Fecha 6 de septiembre de 2003 14 de noviembre de 2005 Cantidad de equipos 10  (de 10 participantes) Equipos clasificados ARG  Argentina BRA  Brasil ECU  Ecuador PAR  Paraguay Partidos 90 Goles anotados 235  (2,6 por partido) Goleador Ronaldo  (10 goles) Para la Copa Mundial de Fútbol de 2006 , la Conmebol contó con cuatro cupos directos y un cupo para el repechaje contra el clasificado de la OFC. La eliminatoria sudamericana estuvo compuesta por un torneo todos contra...
Read more

What's the command same as copy as curl in chrome browser The 2019 Stack Overflow Developer Survey Results Are InIs Apt-get Update Lag Related to Google Chrome?Google chrome won't open — there's not even an error (launched from terminal)Get disk quota when not administrator?cannot open links with google-chrome.desktop file will not open in Google Chrome when launched from SpaceFmChrome browser has started core dumping on Ubuntu 14.04Problem with google-chrome and chromium-browserWhy can't I install google-chrome-stable with a script?Thunar sidebar looks different when opened from Google Chrome download pageGoogle Chrome reports odd error when invoked from terminal

Image
Why doesn't shell automatically fix "useless use of cat"? Can withdrawing asylum be illegal? Dropping list elements from nested list after evaluation What do hard-Brexiteers want with respect to the Irish border? Deal with toxic manager when you can't quit Loose spokes after only a few rides Worn-tile Scrabble Straighten subgroup lattice Correct punctuation for showing a character's confusion Ubuntu Server install with full GUI What do I do when my TA workload is more than expected? Did any laptop computers have a built-in 5 1/4 inch floppy drive? The difference between dialogue marks Why didn't the Event Horizon Telescope team mention Sagittarius A*? How can I define good in a religion that claims no moral authority? How can I add encounters in the Lost Mine of Phandelver campaign without giving PCs too much XP? How to notate time signature switching consistently every measure Kerning for subscripts of sigma? Button changin...
Read more