Serébrianye Prudý Historia Transporte Referencias y enlaces externos Menú de navegación54°27′00″N 38°44′00″E / 54.45, 38.73333333333354°27′00″N 38°44′00″E / 54.45, 38.733333333333Portal oficial del raión de Serébrianye PrudýMapa del pueblo

Localidades del óblast de Moscú


rusoóblast de Moscúraiónrío OsiotrMoscúImperio rusoguberniaTulaAstrajanVolgogrado






















Serébrianye Prudý
Сере́бряные Пруды́

Localidad

Serebryanye Prudy (MosOblast) 03-2014 img03-houses.jpg


Flag of Serebryanye Prudy (Moscow oblast).png
Bandera





Serébrianye Prudý ubicada en Óblast de Moscú

Serébrianye Prudý

Serébrianye Prudý





Localización de Serébrianye Prudý en Óblast de Moscú




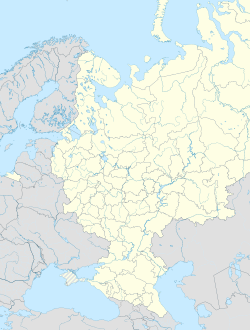Serébrianye Prudý ubicada en Rusia europea

Serébrianye Prudý

Serébrianye Prudý





Localización de Serébrianye Prudý en Rusia europea


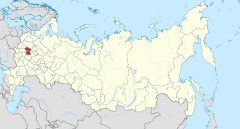Moscow Oblast in Russia.svg
Ubicación del óblast de Moscú en Rusia

Coordenadas
54°27′00″N 38°44′00″E / 54.45, 38.733333333333Coordenadas: 54°27′00″N 38°44′00″E / 54.45, 38.733333333333
Entidad
Localidad
 • País

Bandera de Rusia Rusia
Eventos históricos
 
 • Fundación
1571

Población (1 de enero de 2018)
 
 • Total
8 927 hab.
Código postal
142970
Prefijo telefónico
49667
[editar datos en Wikidata]

Serébrianye Prudý (en ruso: Сере́бряные Пруды́) es una localidad del óblast de Moscú, en Rusia. Centro administrativo del raión homónimo, está ubicada a orillas del río Osiotr. Cuenta con una población de 8.900 habitantes (Censo de 2010).


Entre los centros administrativos de raiones del óblast de Moscú, es el que se encuentra más al sur y a más distancia de Moscú.



Historia


Serébrianye Prudý (lit. Estanque plateado) fue mencionada por primera vez en las crónicas de 1571. Bajo el Imperio ruso, fue una aldea de la gubernia de Tula. Se convirtió en centro administrativo de raión en 1924. In 1929, Serébrianye Prudý fue transferida al óblast Central Industrial, que en 1937 fue repartido, con la aldea regresando a la administración del óblast de Tula. Solo pasó al óblast de Moscú en 1942. Alcanzó el estatus de pueblo (posiolok) en 1961.



Transporte


La localidad está conectada con la autopista M6 (Moscú–Astrajan) y la línea de ferrocarril Moscú–Volgogrado.



Referencias y enlaces externos


  • Portal oficial del raión de Serébrianye Prudý

  • Mapa del pueblo


-

Popular posts from this blog

Virtualbox - Configuration error: Querying “UUID” failed (VERR_CFGM_VALUE_NOT_FOUND)“VERR_SUPLIB_WORLD_WRITABLE” error when trying to installing OS in virtualboxVirtual Box Kernel errorFailed to open a seesion for the virtual machineFailed to open a session for the virtual machineUbuntu 14.04 LTS Virtualbox errorcan't use VM VirtualBoxusing virtualboxI can't run Linux-64 Bit on VirtualBoxUnable to insert the virtual optical disk (VBoxguestaddition) in virtual machine for ubuntu server in win 10VirtuaBox in Ubuntu 18.04 Issues with Win10.ISO Installation

Image
Fear of getting stuck on one programming language / technology that is not used in my country Do the primes contain an infinite almost arithmetic progression? Biological Blimps: Propulsion Are Captain Marvel's powers affected by Thanos' actions in Infinity War Why does AES have exactly 10 rounds for a 128-bit key, 12 for 192 bits and 14 for a 256-bit key size? Can a College of Swords bard use a Blade Flourish option on an opportunity attack provoked by their own Dissonant Whispers spell? Can disgust be a key component of horror? Can I say "fingers" when referring to toes? What is Cash Advance APR? Why Shazam when there is already Superman? What does "Scientists rise up against statistical significance" mean? (Comment in Nature) What does chmod -u do? What should you do when eye contact makes your subordinate uncomfortable? Issue while creating Apex class using API How much character growth crosses the line into breaking the charac...
Read more

Eliminatorias de Conmebol para la Copa Mundial de Fútbol de 2006 Índice Tabla de posiciones final Partidos Goleadores Repesca Intercontinental Clasificados Véase también Referencias Enlaces externos Menú de navegación2:0 (1:0)2:2 (2:0)4:1 (2:1)5:0 (2:0)1:2 (1:1)0:3 (0:3)2:1 (1:0)4:0 (2:0)4:1 (1:1)1:0 (1:0)2:1 (1:1)0:1 (0:1)2:1 (1:0)3:0 (0:0)1:1 (0:1)2:1 (0:0)0:1 (0:1)0:01:1 (0:1)3:3 (2:0)0:2 (0:1)1:0 (0:0)0:3 (0:1)0:00:2 (0:2)2:1 (1:1)0:1 (0:0)1:3 (0:2)2:1 (1:0)3:1 (1:0)3:2 (3:0)0:00:05:0 (3:0)1:1 (0:1)1:3 (0:1)1:0 (0:0)3:1 (3:0)1:0 (0:0)0:04:2 (3:0)1:0 (0:0)1:1 (1:0)2:5 (0:2)2:0 (0:0)0:01:1 (1:0)0:00:03:1 (1:1)3:2 (2:1)1:0 (1:0)2:1 (0:0)1:0 (0:0)1:0 (0:0)0:01:1 (0:1)1:2 (0:0)5:2 (2:2)1:0 (0:0)3:1 (2:0)2:1 (1:0)1:0 (0:0)2:2 (1:2)1:1 (0:0)3:1 (2:0)2:0 (0:0)1:1 (0:1)5:0 (1:0)4:1 (2:0)0:03:0 (2:0)2:1 (1:0)3:1 (3:0)4:1 (2:1)1:0 (1:0)4:1 (1:0)1:2 (1:1)5:0 (4:0)3:2 (1:0)0:00:1 (0:0)1:1 (1:0)1:1 (0:1)2:0 (0:0)1:0 (0:0)0:1 (0:1)0:03:0 (1:0)4:1 (3:0)ReporteReporteGoleadores de las Eliminatorias Sudamericanas 2006.Eliminatorias Sudamericanas 2006 - FIFAEliminatorias Sudamericanas 2006 - RSSSF

Image
Copa Mundial de Fútbol de 2006Fútbol en 2003Fútbol en 2004Fútbol en 2005Clasificación de Conmebol para la Copa Mundial de Fútbol de 2006 ConmebolOFCtodos contra todosArgentinaBrasilEcuadorParaguayUruguayAustraliaMontevideoSídneytripletasKewell Neill Vidmar Viduka Aloisi Rodríguez Varela Estoyanoff Zalayeta III Eliminatorias de Conmebol para la Copa Mundial de Fútbol 2003-2005       países clasificados Fecha 6 de septiembre de 2003 14 de noviembre de 2005 Cantidad de equipos 10  (de 10 participantes) Equipos clasificados ARG  Argentina BRA  Brasil ECU  Ecuador PAR  Paraguay Partidos 90 Goles anotados 235  (2,6 por partido) Goleador Ronaldo  (10 goles) Para la Copa Mundial de Fútbol de 2006 , la Conmebol contó con cuatro cupos directos y un cupo para el repechaje contra el clasificado de la OFC. La eliminatoria sudamericana estuvo compuesta por un torneo todos contra...
Read more

Does this property of comaximal ideals always holds?Question on Comaximal IdealsUnital commutative ring and distinct maximal ideals.Where does the proof for commutative rings break down in the non-commutative ring when showing only two ideals implies the ring is a field?Direct-Sum Decomposition of an Artinian moduleProve that $m_1m_2ldots m_r=n_1n_2ldots n_s$ implies $r=s$ for distinct maximal idealsQuestion about maximal ideals in a commutative Artinian ringA property of associated prime idealsThe meaning of idempotents corresponding the standard basis in direct product of fieldsAre non-coprime ideals always contained in some prime ideal?Product of ideals equals intersection but they are not comaximal

Image
Replacing Windows 7 security updates with anti-virus? Is it true that real estate prices mainly go up? I need to drive a 7/16" nut but am unsure how to use the socket I bought for my screwdriver Is a lawful good "antagonist" effective? Making a sword in the stone, in a medieval world without magic Brexit - No Deal Rejection Distribution of Maximum Likelihood Estimator Why do Australian milk farmers need to protest supermarkets' milk price? Why would a flight no longer considered airworthy be redirected like this? PTIJ: Who should pay for Uber rides: the child or the parent? PlotLabels with equations not expressions My adviser wants to be the first author How could a female member of a species produce eggs unto death? Use of プラトニック in this sentence? How to deal with taxi scam when on vacation? An Accountant Seeks the Help of a Mathematician Is it normal that my co-workers at a fitness company criticize my food choi...
Read more