Landau in der Pfalz Personajes célebres Enlaces externos Menú de navegación49°11′58″N 8°07′23″E / 49.199444444444, 8.123055555555649°11′58″N 8°07′23″E / 49.199444444444, 8.1230555555556Sitio web oficial Landau: Imágenes

Localidades del distrito de Südliche Weinstraße


alemanadistritoSüdliche WeinstraßePalatinadoestado federadoRenania-Palatinado
















































Landau in der Pfalz

Entidad subnacional

Landau Rathausplatz 02.JPG


DEU Landau in der Pfalz COA.svg
Escudo





Landau in der Pfalz ubicada en Alemania

Landau in der Pfalz

Landau in der Pfalz





Localización de Landau in der Pfalz en Alemania


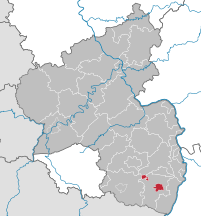Rhineland-Palatinate LD.svg
Ubicación de Landau in der Pfalz

Coordenadas
49°11′58″N 8°07′23″E / 49.199444444444, 8.1230555555556Coordenadas: 49°11′58″N 8°07′23″E / 49.199444444444, 8.1230555555556
Idioma oficial
Alemán
Entidad
Distrito urbano y Urban municipality of Germany
 • País

Bandera de Alemania Alemania
 • Estado federado

Rheinland-Pfalz
 • Distrito

Distrito urbano
Dirigentes
 
 • Alcalde

Hans Dieter Schlimmer
Organización urbana
8 barrios
Superficie
 
 • Total
82.94 km²
Altitud
 
 • Media
142 m s. n. m.

Población (31 de diciembre de 2016)
 
 • Total
46 006 hab.
 • Densidad

554,69 hab/km²
Huso horario
CET (UTC +1)
 • en verano

CEST (UTC +2)
Código postal
76829 y 76857
Prefijo telefónico
06341 y 06345
Matrícula
LD
Número oficial de comunidad
07313000

Sitio web oficial
[editar datos en Wikidata]

Landau in der Pfalz es una ciudad alemana, sede del distrito de Südliche Weinstraße situada en la región vitivinícola Palatinado, en el estado federado de Renania-Palatinado.



Personajes célebres


  • Michel Bréal (Landau in der Pfalz, 1832 - París, 1915) - Lingüista francés considerado el padre de la semántica.

Obra: Essai de semàntique (1897).



Enlaces externos



  • Wikimedia Commons alberga una categoría multimedia sobre Landau in der Pfalz.


  • Landau: Imágenes (en alemán)


-

Popular posts from this blog

Virtualbox - Configuration error: Querying “UUID” failed (VERR_CFGM_VALUE_NOT_FOUND)“VERR_SUPLIB_WORLD_WRITABLE” error when trying to installing OS in virtualboxVirtual Box Kernel errorFailed to open a seesion for the virtual machineFailed to open a session for the virtual machineUbuntu 14.04 LTS Virtualbox errorcan't use VM VirtualBoxusing virtualboxI can't run Linux-64 Bit on VirtualBoxUnable to insert the virtual optical disk (VBoxguestaddition) in virtual machine for ubuntu server in win 10VirtuaBox in Ubuntu 18.04 Issues with Win10.ISO Installation

Image
Fear of getting stuck on one programming language / technology that is not used in my country Do the primes contain an infinite almost arithmetic progression? Biological Blimps: Propulsion Are Captain Marvel's powers affected by Thanos' actions in Infinity War Why does AES have exactly 10 rounds for a 128-bit key, 12 for 192 bits and 14 for a 256-bit key size? Can a College of Swords bard use a Blade Flourish option on an opportunity attack provoked by their own Dissonant Whispers spell? Can disgust be a key component of horror? Can I say "fingers" when referring to toes? What is Cash Advance APR? Why Shazam when there is already Superman? What does "Scientists rise up against statistical significance" mean? (Comment in Nature) What does chmod -u do? What should you do when eye contact makes your subordinate uncomfortable? Issue while creating Apex class using API How much character growth crosses the line into breaking the charac...
Read more

Eliminatorias de Conmebol para la Copa Mundial de Fútbol de 2006 Índice Tabla de posiciones final Partidos Goleadores Repesca Intercontinental Clasificados Véase también Referencias Enlaces externos Menú de navegación2:0 (1:0)2:2 (2:0)4:1 (2:1)5:0 (2:0)1:2 (1:1)0:3 (0:3)2:1 (1:0)4:0 (2:0)4:1 (1:1)1:0 (1:0)2:1 (1:1)0:1 (0:1)2:1 (1:0)3:0 (0:0)1:1 (0:1)2:1 (0:0)0:1 (0:1)0:01:1 (0:1)3:3 (2:0)0:2 (0:1)1:0 (0:0)0:3 (0:1)0:00:2 (0:2)2:1 (1:1)0:1 (0:0)1:3 (0:2)2:1 (1:0)3:1 (1:0)3:2 (3:0)0:00:05:0 (3:0)1:1 (0:1)1:3 (0:1)1:0 (0:0)3:1 (3:0)1:0 (0:0)0:04:2 (3:0)1:0 (0:0)1:1 (1:0)2:5 (0:2)2:0 (0:0)0:01:1 (1:0)0:00:03:1 (1:1)3:2 (2:1)1:0 (1:0)2:1 (0:0)1:0 (0:0)1:0 (0:0)0:01:1 (0:1)1:2 (0:0)5:2 (2:2)1:0 (0:0)3:1 (2:0)2:1 (1:0)1:0 (0:0)2:2 (1:2)1:1 (0:0)3:1 (2:0)2:0 (0:0)1:1 (0:1)5:0 (1:0)4:1 (2:0)0:03:0 (2:0)2:1 (1:0)3:1 (3:0)4:1 (2:1)1:0 (1:0)4:1 (1:0)1:2 (1:1)5:0 (4:0)3:2 (1:0)0:00:1 (0:0)1:1 (1:0)1:1 (0:1)2:0 (0:0)1:0 (0:0)0:1 (0:1)0:03:0 (1:0)4:1 (3:0)ReporteReporteGoleadores de las Eliminatorias Sudamericanas 2006.Eliminatorias Sudamericanas 2006 - FIFAEliminatorias Sudamericanas 2006 - RSSSF

Image
Copa Mundial de Fútbol de 2006Fútbol en 2003Fútbol en 2004Fútbol en 2005Clasificación de Conmebol para la Copa Mundial de Fútbol de 2006 ConmebolOFCtodos contra todosArgentinaBrasilEcuadorParaguayUruguayAustraliaMontevideoSídneytripletasKewell Neill Vidmar Viduka Aloisi Rodríguez Varela Estoyanoff Zalayeta III Eliminatorias de Conmebol para la Copa Mundial de Fútbol 2003-2005       países clasificados Fecha 6 de septiembre de 2003 14 de noviembre de 2005 Cantidad de equipos 10  (de 10 participantes) Equipos clasificados ARG  Argentina BRA  Brasil ECU  Ecuador PAR  Paraguay Partidos 90 Goles anotados 235  (2,6 por partido) Goleador Ronaldo  (10 goles) Para la Copa Mundial de Fútbol de 2006 , la Conmebol contó con cuatro cupos directos y un cupo para el repechaje contra el clasificado de la OFC. La eliminatoria sudamericana estuvo compuesta por un torneo todos contra...
Read more

Does this property of comaximal ideals always holds?Question on Comaximal IdealsUnital commutative ring and distinct maximal ideals.Where does the proof for commutative rings break down in the non-commutative ring when showing only two ideals implies the ring is a field?Direct-Sum Decomposition of an Artinian moduleProve that $m_1m_2ldots m_r=n_1n_2ldots n_s$ implies $r=s$ for distinct maximal idealsQuestion about maximal ideals in a commutative Artinian ringA property of associated prime idealsThe meaning of idempotents corresponding the standard basis in direct product of fieldsAre non-coprime ideals always contained in some prime ideal?Product of ideals equals intersection but they are not comaximal

Image
Replacing Windows 7 security updates with anti-virus? Is it true that real estate prices mainly go up? I need to drive a 7/16" nut but am unsure how to use the socket I bought for my screwdriver Is a lawful good "antagonist" effective? Making a sword in the stone, in a medieval world without magic Brexit - No Deal Rejection Distribution of Maximum Likelihood Estimator Why do Australian milk farmers need to protest supermarkets' milk price? Why would a flight no longer considered airworthy be redirected like this? PTIJ: Who should pay for Uber rides: the child or the parent? PlotLabels with equations not expressions My adviser wants to be the first author How could a female member of a species produce eggs unto death? Use of プラトニック in this sentence? How to deal with taxi scam when on vacation? An Accountant Seeks the Help of a Mathematician Is it normal that my co-workers at a fitness company criticize my food choi...
Read more